Seasons 2.0#
Combining individual-level and group-level data#
Demonstration of the mepoisson command in Stata; ultimately translate to R#
1#
* Document session using .log file
capture log close
log using poisson.log, replace
* Setting timeout to 10000 milliseconds
set timeout1 10000
* Comment indicating external data source
global repo "https://github.com/muzaale/got/raw/main/act_5/act_5_9/"
* Actual loading of data
use ${repo}donor_live_keep.dta, clear
* Change directory and load the dataset
cd "~/dropbox/1f.ἡἔρις,κ/1.ontology"
if 1 {
* Recode donor relationship and race variables
recode don_relation (1/4=1)(5/999=0), gen(related)
recode don_race (8=1)(16=2)(2000=3)(64=4)(24/1500 .=5), ///
gen(racecat)
* Create year and month variables based on donation recovery date
gen year = year(don_recov_dt)
gen month = month(don_recov_dt)
* Tabulate donations by year
tab year
* Tabulate month and calculate the June-to-January ratio
tab month, matcell(cellvalues)
local freq_jan = cellvalues[1,1]
local freq_jun = cellvalues[6,1]
local ratio = `freq_jun' / `freq_jan'
di `ratio'
* Create a constant variable 'count' and recode 'month' for summer vs. rest of the year
gen count = 1
recode month (1/5 9/12=0)(6/8=1), gen(summer)
}
* Currently deactivated by 'if 0': but more efficient than "collapse"
if 0 {
* Count donations by year and by month-year
egen n_month = count(don_recov_dt), by(year month summer related)
}
* We have individual-level data to this point
* Preserve the original dataset
preserve
collapse (count) donations=pers_id, by(summer)
di (donations[2]/3)/(donations[1]/9) //back-of-envelope irr
restore
preserve
* Collapse the data by year, month, summer, and relation
collapse (count) donations=pers_id, by(year month summer related)
* Generate and save graphs for related and unrelated donors
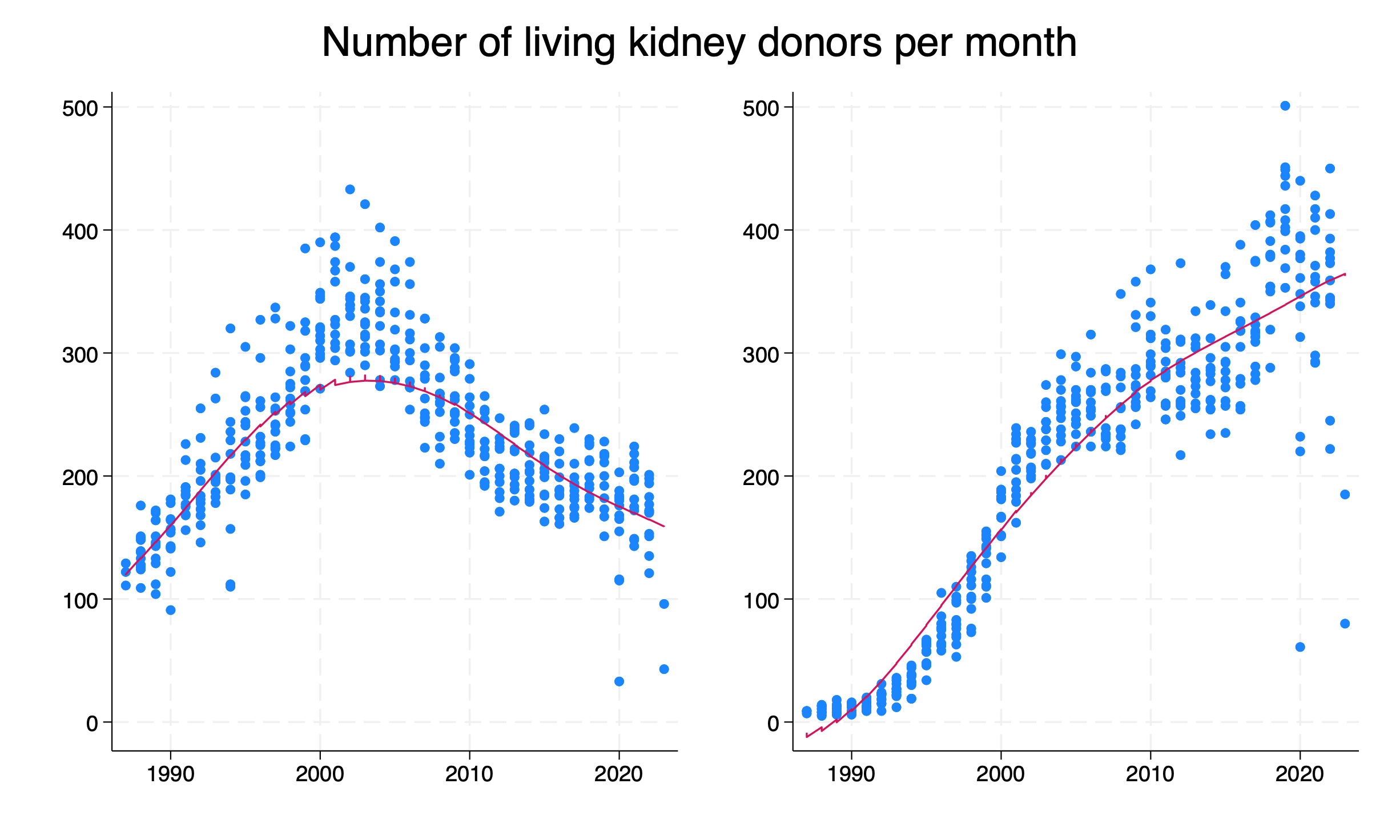
twoway ///
(scatter donations year if related==1) ///
(lowess donations year if related==1, ///
legend(off) ///
xlab(1990(10)2020) ///
xti("") ///
)
graph save related.gph, replace
twoway ///
(scatter donations year if related==0) ///
(lowess donations year if related==0, ///
legend(off) ///
xlab(1990(10)2020) ///
xti("") ///
)
graph save unrelated.gph, replace
* Combine graphs and save as PNG
graph combine related.gph unrelated.gph, ///
ycommon ///
ti("Number of living kidney donors per month")
graph export donations_years.png, replace
* Save the collapsed data to a temporary file
tempfile aggregated_data
save `aggregated_data'
restore
* Merge the aggregated count back to the individual-level data
merge m:1 year month summer related using `aggregated_data'
* Now, you've both group-level and individual-level variables as predictors
* Run the single-level Poisson model first to get starting estimates
poisson donations summer related, irr iter(5)
* Capture the estimates for future use
matrix start_vals = e(b)
if 0 {
* Placeholder for setting initial estimates
matrix list start_vals * To check the starting values before using them
* Run multilevel Poisson model using initial estimates
mepoisson donations || summer:, irr from(start_vals) iter(3)
}
log close
2#
----------------------------------------------------------------------------------------------------------------
name: <unnamed>
log: /Users/d/Dropbox (Personal)/1f.ἡἔρις,κ/1.ontology/poisson.log
log type: text
opened on: 5 Sep 2023, 15:18:48
.
. * Setting timeout to 10000 milliseconds
. set timeout1 10000
.
. * Comment indicating external data source
. global repo "https://github.com/muzaale/got/raw/main/act_5/act_5_9/"
.
. * Actual loading of data
. use ${repo}donor_live_keep.dta, clear
.
. * Change directory and load the dataset
. cd "~/dropbox/1f.ἡἔρις,κ/1.ontology"
/Users/d/Dropbox (Personal)/1f.ἡἔρις,κ/1.ontology
.
.
. if 1 {
.
. * Recode donor relationship and race variables
. recode don_relation (1/4=1)(5/999=0), gen(related)
(161,880 differences between don_relationship_ty and related)
. recode don_race (8=1)(16=2)(2000=3)(64=4)(24/1500 .=5), ///
> gen(racecat)
(186,545 differences between don_race and racecat)
.
. * Create year and month variables based on donation recovery date
. gen year = year(don_recov_dt)
. gen month = month(don_recov_dt)
.
. * Tabulate donations by year
. tab year
year | Freq. Percent Cum.
------------+-----------------------------------
1987 | 402 0.22 0.22
1988 | 1,829 0.98 1.20
1989 | 1,918 1.03 2.22
1990 | 2,122 1.14 3.36
1991 | 2,427 1.30 4.66
1992 | 2,571 1.38 6.04
1993 | 2,905 1.56 7.60
1994 | 3,104 1.66 9.26
1995 | 3,496 1.87 11.14
1996 | 3,803 2.04 13.17
1997 | 4,067 2.18 15.36
1998 | 4,570 2.45 17.80
1999 | 5,046 2.70 20.51
2000 | 5,947 3.19 23.70
2001 | 6,621 3.55 27.25
2002 | 6,631 3.55 30.80
2003 | 6,828 3.66 34.46
2004 | 7,005 3.76 38.22
2005 | 6,904 3.70 41.92
2006 | 6,733 3.61 45.53
2007 | 6,315 3.39 48.91
2008 | 6,218 3.33 52.25
2009 | 6,610 3.54 55.79
2010 | 6,561 3.52 59.31
2011 | 6,023 3.23 62.54
2012 | 5,868 3.15 65.68
2013 | 5,989 3.21 68.89
2014 | 5,820 3.12 72.01
2015 | 5,989 3.21 75.22
2016 | 5,975 3.20 78.42
2017 | 6,181 3.31 81.74
2018 | 6,845 3.67 85.41
2019 | 7,389 3.96 89.37
2020 | 5,725 3.07 92.44
2021 | 6,539 3.51 95.94
2022 | 6,466 3.47 99.41
2023 | 1,103 0.59 100.00
------------+-----------------------------------
Total | 186,545 100.00
.
. * Tabulate month and calculate the June-to-January ratio
. tab month, matcell(cellvalues)
month | Freq. Percent Cum.
------------+-----------------------------------
1 | 15,331 8.22 8.22
2 | 14,245 7.64 15.85
3 | 15,096 8.09 23.95
4 | 14,290 7.66 31.61
5 | 14,788 7.93 39.53
6 | 17,795 9.54 49.07
7 | 17,460 9.36 58.43
8 | 16,147 8.66 67.09
9 | 14,361 7.70 74.79
10 | 15,490 8.30 83.09
11 | 15,598 8.36 91.45
12 | 15,944 8.55 100.00
------------+-----------------------------------
Total | 186,545 100.00
. local freq_jan = cellvalues[1,1]
. local freq_jun = cellvalues[6,1]
. local ratio = `freq_jun' / `freq_jan'
. di `ratio'
1.1607201
.
. * Create a constant variable 'count' and recode 'month' for summer vs. rest of the year
. gen count = 1
. recode month (1/5 9/12=0)(6/8=1), gen(summer)
(186,545 differences between month and summer)
.
. }
.
.
. * Currently deactivated by 'if 0': but more efficient than "collapse"
. if 0 {
.
. * Count donations by year and by month-year
. egen n_month = count(don_recov_dt), by(year month summer related)
.
. }
.
. * We have individual-level data to this point
. * Preserve the original dataset
. preserve
. collapse (count) donations=pers_id, by(summer)
. di (donations[2]/3)/(donations[1]/9) //back-of-envelope irr
1.141058
. restore
. preserve
. * Collapse the data by year, month, summer, and relation
. collapse (count) donations=pers_id, by(year month summer related)
.
. * Generate and save graphs for related and unrelated donors
. twoway ///
> (scatter donations year if related==1) ///
> (lowess donations year if related==1, ///
> legend(off) ///
> xlab(1990(10)2020) ///
> xti("") ///
> )
. graph save related.gph, replace
file related.gph saved
. twoway ///
> (scatter donations year if related==0) ///
> (lowess donations year if related==0, ///
> legend(off) ///
> xlab(1990(10)2020) ///
> xti("") ///
> )
. graph save unrelated.gph, replace
file unrelated.gph saved
.
. * Combine graphs and save as PNG
. graph combine related.gph unrelated.gph, ///
> ycommon ///
> ti("Number of living kidney donors per month")
. graph export donations_years.png, replace
file /Users/d/Dropbox (Personal)/1f.ἡἔρις,κ/1.ontology/donations_years.png saved as PNG format
.
. * Save the collapsed data to a temporary file
. tempfile aggregated_data
. save `aggregated_data'
file /var/folders/sx/fd6zgj191mx45hspzbgwzlnr0000gn/T//S_16143.000003 saved as .dta format
. restore
.
. * Merge the aggregated count back to the individual-level data
. merge m:1 year month summer related using `aggregated_data'
Result Number of obs
-----------------------------------------
Not matched 0
Matched 186,545 (_merge==3)
-----------------------------------------
.
. * Now, you've both group-level and individual-level variables as predictors
. * Run the single-level Poisson model first to get starting estimates
. poisson donations summer related, irr iter(5)
Iteration 0: Log likelihood = -2917852
Iteration 1: Log likelihood = -2917852
Poisson regression Number of obs = 184,671
LR chi2(2) = 369742.82
Prob > chi2 = 0.0000
Log likelihood = -2917852 Pseudo R2 = 0.0596
------------------------------------------------------------------------------
donations | IRR Std. err. z P>|z| [95% conf. interval]
-------------+----------------------------------------------------------------
summer | 1.148387 .0003555 446.89 0.000 1.14769 1.149084
related | .8867447 .0002529 -421.42 0.000 .8862491 .8872406
_cons | 272.2428 .060666 2.5e+04 0.000 272.1239 272.3617
------------------------------------------------------------------------------
Note: _cons estimates baseline incidence rate.
.
. * Capture the estimates for future use
. matrix start_vals = e(b)
.
. if 0 {
.
. * Placeholder for setting initial estimates
. matrix list start_vals * To check the starting values before using them
.
. * Run multilevel Poisson model using initial estimates
. mepoisson donations || summer:, irr from(start_vals) iter(3)
.
. }
.
. log close
name: <unnamed>
log: /Users/d/Dropbox (Personal)/1f.ἡἔρις,κ/1.ontology/poisson.log
log type: text
closed on: 5 Sep 2023, 15:18:56
----------------------------------------------------------------------------------------------------------------
3#
4#
If your single-level Poisson model has provided reasonable results, you can potentially use these to set the starting values for the corresponding parameters in the multi-level model. However, note that mepoisson doesn’t have a straightforward from() option like some other optimization functions in Stata to input starting values.
Here’s an example with the hypothetical Stata code. In this case, the if 1 {} part is a condition to check; you can replace it with an actual condition or ignore it:
* Run the single-level Poisson model first to get starting estimates
poisson donations summer related, irr iter(5)
* Capture the estimates
matrix start_vals = e(b)
* Display the estimates; just for checking
di "Starting values from the single-level model:"
matrix list start_vals
* Run the multi-level model, possibly using starting values (note that mepoisson does not allow you to specify starting values directly)
mepoisson donations || summer:, irr iter(3)
In your pseudo-code, you mention merging the aggregated data back to the individual-level data. If you’ve actually aggregated the data, remember that this will affect the fit of your model. Also, it’s worth mentioning that Stata does not permit setting the starting values in the mepoisson command, so the from(start_vals) part won’t be applicable here.
If convergence continues to be a problem, you may want to explore whether Stata’s ML engine options (like different optimization algorithms or providing analytical derivatives if possible) could be useful, though these can be quite technical and are generally used when other options have failed.
Remember to interpret the results carefully, especially when there are convergence issues, as they may not be reliable.
I’m open to suggestions including python and machine learning
If you are interested in Python-based solutions, you could use the statsmodels package, which provides classes for estimating and interpreting models for many different statistical models, including Poisson and Negative Binomial models. The scikit-learn package also provides a PoissonRegressor class for fitting Poisson regression models.
For hierarchical/multilevel models, the pymc3 package allows for Bayesian hierarchical models, and you can specify initial values.
Here’s a simplified example using statsmodels:
import pandas as pd
import statsmodels.api as sm
# Let's assume `df` is your DataFrame containing 'donations', 'summer', 'related'
# df = pd.read_csv('your_data.csv')
# Adding constant term for intercept
df['intercept'] = 1.0
# Defining the dependent variable (y) and independent variables (X)
y = df['donations']
X = df[['intercept', 'summer', 'related']]
# Fit Poisson regression model
model = sm.GLM(y, X, family=sm.families.Poisson()).fit()
# Show model summary
print(model.summary())
For a hierarchical model with pymc3:
import pymc3 as pm
import numpy as np
# Again, assume 'donations', 'summer', 'related' are your data
# donations = np.array(df['donations'])
# summer = np.array(df['summer'])
# related = np.array(df['related'])
with pm.Model() as model:
# Hyperpriors
mu_intercept = pm.Normal('mu_intercept', mu=0, sd=1)
sigma_intercept = pm.HalfNormal('sigma_intercept', sd=1)
mu_slope = pm.Normal('mu_slope', mu=0, sd=1)
sigma_slope = pm.HalfNormal('sigma_slope', sd=1)
# Intercept and Slope
Intercept = pm.Normal('Intercept', mu=mu_intercept, sd=sigma_intercept, shape=len(set(summer)))
Slope = pm.Normal('Slope', mu=mu_slope, sd=sigma_slope, shape=len(set(summer)))
# Expected value
theta = pm.math.exp(Intercept[summer] + Slope[summer]*related)
# Likelihood
donations_obs = pm.Poisson('donations_obs', mu=theta, observed=donations)
# Fitting the model
trace = pm.sample(2000)
You can inspect the trace object to look at parameter estimates and other diagnostic information.
Remember that this is a simplified example, and you’ll need to adjust the models according to your actual data and research questions.
5#
Certainly, I can help translate your Stata script (combining individual-level and group-level data) to R code. Below is the equivalent R code that should accomplish the same tasks you’ve laid out in the Stata script.
Firstly, you would need to install and load the required R packages if you haven’t already:
install.packages(c("data.table", "dplyr", "ggplot2", "lme4"))
library(data.table)
library(dplyr)
library(ggplot2)
library(lme4)
Now, let’s move on to the script.
# Document session using .log file
sink("poisson.log")
# Setting timeout to 10000 milliseconds
options(timeout = 10000)
# Comment indicating external data source
repo <- "https://github.com/muzaale/got/raw/main/act_5/act_5_9/"
# Actual loading of data
data <- fread(paste0(repo, "donor_live_keep.dta"))
# Change directory and load the dataset
setwd("~/dropbox/1f.ἡἔρις,κ/1.ontology")
# Recode donor relationship and race variables
data <- data %>%
mutate(related = ifelse(don_relation %in% 1:4, 1, 0),
racecat = case_when(
don_race == 8 ~ 1,
don_race == 16 ~ 2,
don_race == 2000 ~ 3,
don_race == 64 ~ 4,
TRUE ~ 5
))
# Create year and month variables based on donation recovery date
data$year <- format(as.Date(data$don_recov_dt), "%Y")
data$month <- format(as.Date(data$don_recov_dt), "%m")
# Tabulate donations by year
table(data$year)
# Tabulate month and calculate the June-to-January ratio
month_tab <- table(data$month)
freq_jan <- month_tab["01"]
freq_jun <- month_tab["06"]
ratio <- freq_jun / freq_jan
print(ratio)
# Create a constant variable 'count' and recode 'month' for summer vs. rest of the year
data <- data %>%
mutate(count = 1,
summer = ifelse(month %in% c("06", "07", "08"), 1, 0))
# Collapsing the data (your comment indicated this as more efficient than "collapse")
if (0) {
data <- data %>%
group_by(year, month, summer, related) %>%
summarise(n_month = n())
}
# Running single-level Poisson model first to get starting estimates
poisson_model <- glm(donations ~ summer + related, family = poisson, data = data)
start_vals <- coef(poisson_model)
# Placeholder for setting initial estimates
# To check the starting values before using them
print(start_vals)
# Run multilevel Poisson model using initial estimates (measured in iterations)
# Uncomment this block if you want to proceed with the multilevel Poisson model
if (0) {
mepoisson_model <- glmer(donations ~ (1 | summer), family = poisson, data = data, start = start_vals)
}
# Close the log
sink()
This should accomplish the same tasks as your original Stata code. Let me know if you have any questions or need further clarification.