Show code cell source
import numpy as np
import pandas as pd
from scipy.stats import multivariate_normal, expon
def correlation_to_covariance(correlation, std_dev):
covariance = np.outer(std_dev, std_dev) * correlation
return covariance
def simulate_data(n=1000, study_duration=25):
np.random.seed(42)
# Define the correlation matrix and standard deviations
correlation = np.array([
[1.0, 0.5, 0.2, 0.3],
[0.5, 1.0, 0.3, 0.4],
[0.2, 0.3, 1.0, 0.1],
[0.3, 0.4, 0.1, 1.0]
])
std_dev = np.array([10, 15, 0.5, 5])
cov = correlation_to_covariance(correlation, std_dev)
mean = [60, 120, 1, 25]
age, sbp, scr, bmi = multivariate_normal.rvs(mean=mean, cov=cov, size=n).T
# Other variables
hba1c = np.random.normal(5, 1, n)
hypertension = np.random.randint(2, size=n)
smoke = np.random.randint(2, size=n)
racecat = np.random.choice(['Black', 'Hispanic', 'Other', 'White'], n)
educat = np.random.choice(['High School', 'K-8', 'Some college'], n)
male = np.random.randint(2, size=n)
# Simulate time to kidney failure using a log-normal distribution
median_time_to_failure = 15
mean_time_to_failure = 19
sigma = np.sqrt(np.log(mean_time_to_failure**2 / median_time_to_failure**2))
mu = np.log(median_time_to_failure)
time_to_kidney_failure = np.random.lognormal(mean=mu, sigma=sigma, size=n)
time_to_kidney_failure = np.clip(time_to_kidney_failure, 0.1, 30)
# Simulate censoring times using an exponential distribution
censoring_times = expon.rvs(scale=study_duration, size=n)
observed_times = np.minimum(time_to_kidney_failure, censoring_times)
status = (time_to_kidney_failure <= censoring_times).astype(int)
# Create a DataFrame
df = pd.DataFrame({
'age': age,
'sbp': sbp,
'scr': scr,
'bmi': bmi,
'hba1c': hba1c,
'hypertension': hypertension,
'smoke': smoke,
'race': racecat,
'education': educat,
'male': male,
'time_to_failure': observed_times,
'status': status
})
return df
# Simulate the data
df = simulate_data()
# Save to CSV
df.to_csv("simulated_data_with_censoring.csv", index=False)
# Print summaries
print(df.describe())
age sbp scr bmi hba1c \
count 1000.000000 1000.000000 1000.000000 1000.000000 1000.000000
mean 59.973979 119.472001 1.009669 24.897981 4.950726
std 9.856352 14.501902 0.503815 5.057554 0.992380
min 30.326603 64.838818 -0.466847 8.899264 1.823296
25% 53.111644 109.675974 0.660291 21.504805 4.317395
50% 60.174003 119.788775 1.013048 24.949501 4.981758
75% 66.429221 128.751981 1.347884 28.092598 5.639123
max 97.106483 164.260059 2.739422 40.477585 8.112910
hypertension smoke male time_to_failure status
count 1000.000000 1000.000000 1000.00000 1000.000000 1000.000000
mean 0.505000 0.493000 0.50000 11.227176 0.512000
std 0.500225 0.500201 0.50025 7.928697 0.500106
min 0.000000 0.000000 0.00000 0.025571 0.000000
25% 0.000000 0.000000 0.00000 5.141288 0.000000
50% 1.000000 0.000000 0.50000 9.519271 1.000000
75% 1.000000 1.000000 1.00000 15.464865 1.000000
max 1.000000 1.000000 1.00000 30.000000 1.000000
Show code cell source
# !pip install lifelines
import pandas as pd
from lifelines import CoxPHFitter
# Convert categorical variables to dummies
df_dummies = pd.get_dummies(df, columns=['race', 'education'], drop_first=True)
# Instantiate the Cox Proportional Hazards model
cph = CoxPHFitter()
# Fit the model to the data
cph.fit(df_dummies, duration_col='time_to_failure', event_col='status')
# Print the summary table, which includes HRs and 95% CIs
cph.print_summary()
# Coefficient matrix (log hazard ratios)
coefficients = cph.params_
print("Coefficient Matrix:")
print(coefficients)
# Variance-covariance matrix
variance_covariance_matrix = cph.variance_matrix_
print("Variance-Covariance Matrix:")
print(variance_covariance_matrix)
| model | lifelines.CoxPHFitter |
|---|---|
| duration col | 'time_to_failure' |
| event col | 'status' |
| baseline estimation | breslow |
| number of observations | 1000 |
| number of events observed | 512 |
| partial log-likelihood | -2866.24 |
| time fit was run | 2023-08-17 22:04:12 UTC |
| coef | exp(coef) | se(coef) | coef lower 95% | coef upper 95% | exp(coef) lower 95% | exp(coef) upper 95% | cmp to | z | p | -log2(p) | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| age | -0.01 | 0.99 | 0.01 | -0.02 | -0.00 | 0.98 | 1.00 | 0.00 | -2.65 | 0.01 | 6.96 |
| sbp | -0.00 | 1.00 | 0.00 | -0.01 | 0.01 | 0.99 | 1.01 | 0.00 | -0.08 | 0.94 | 0.09 |
| scr | 0.13 | 1.14 | 0.09 | -0.06 | 0.31 | 0.94 | 1.37 | 0.00 | 1.36 | 0.18 | 2.51 |
| bmi | 0.01 | 1.01 | 0.01 | -0.01 | 0.03 | 0.99 | 1.03 | 0.00 | 0.61 | 0.54 | 0.88 |
| hba1c | -0.05 | 0.95 | 0.04 | -0.13 | 0.04 | 0.88 | 1.04 | 0.00 | -1.06 | 0.29 | 1.80 |
| hypertension | 0.10 | 1.11 | 0.09 | -0.07 | 0.28 | 0.93 | 1.32 | 0.00 | 1.12 | 0.26 | 1.94 |
| smoke | -0.03 | 0.97 | 0.09 | -0.20 | 0.15 | 0.82 | 1.16 | 0.00 | -0.30 | 0.76 | 0.39 |
| male | -0.01 | 0.99 | 0.09 | -0.19 | 0.17 | 0.83 | 1.18 | 0.00 | -0.10 | 0.92 | 0.12 |
| race_Hispanic | 0.18 | 1.20 | 0.13 | -0.06 | 0.43 | 0.94 | 1.54 | 0.00 | 1.48 | 0.14 | 2.84 |
| race_Other | 0.20 | 1.23 | 0.12 | -0.04 | 0.44 | 0.96 | 1.56 | 0.00 | 1.66 | 0.10 | 3.36 |
| race_White | 0.10 | 1.11 | 0.13 | -0.14 | 0.35 | 0.87 | 1.42 | 0.00 | 0.83 | 0.41 | 1.29 |
| education_K-8 | -0.17 | 0.85 | 0.11 | -0.38 | 0.05 | 0.68 | 1.05 | 0.00 | -1.49 | 0.14 | 2.87 |
| education_Some college | -0.13 | 0.88 | 0.11 | -0.34 | 0.08 | 0.71 | 1.08 | 0.00 | -1.23 | 0.22 | 2.18 |
| Concordance | 0.55 |
|---|---|
| Partial AIC | 5758.48 |
| log-likelihood ratio test | 17.00 on 13 df |
| -log2(p) of ll-ratio test | 2.33 |
Coefficient Matrix:
covariate
age -0.013337
sbp -0.000274
scr 0.128553
bmi 0.006206
hba1c -0.046943
hypertension 0.100960
smoke -0.027003
male -0.008717
race_Hispanic 0.184603
race_Other 0.203355
race_White 0.104264
education_K-8 -0.165335
education_Some college -0.132012
Name: coef, dtype: float64
Variance-Covariance Matrix:
covariate age sbp scr bmi hba1c \
covariate
age 0.000025 -0.000006 -0.000075 -0.000007 8.126299e-06
sbp -0.000006 0.000013 -0.000071 -0.000011 -2.379526e-06
scr -0.000075 -0.000071 0.008991 -0.000013 6.076963e-05
bmi -0.000007 -0.000011 -0.000013 0.000104 1.701619e-05
hba1c 0.000008 -0.000002 0.000061 0.000017 1.945850e-03
hypertension 0.000006 0.000003 0.000398 -0.000026 -4.582618e-05
smoke -0.000023 -0.000018 -0.000176 -0.000017 -5.294871e-07
male -0.000056 0.000019 0.000426 0.000024 1.603505e-04
race_Hispanic 0.000006 0.000003 0.000451 0.000048 4.355287e-04
race_Other -0.000051 -0.000019 0.000118 0.000004 1.328256e-04
race_White -0.000036 0.000021 0.000219 -0.000015 3.049609e-04
education_K-8 0.000022 -0.000043 -0.000194 0.000050 -3.356481e-05
education_Some college -0.000008 -0.000050 0.000051 0.000059 -3.188334e-04
covariate hypertension smoke male race_Hispanic \
covariate
age 0.000006 -2.290813e-05 -0.000056 0.000006
sbp 0.000003 -1.776325e-05 0.000019 0.000003
scr 0.000398 -1.757945e-04 0.000426 0.000451
bmi -0.000026 -1.681884e-05 0.000024 0.000048
hba1c -0.000046 -5.294871e-07 0.000160 0.000436
hypertension 0.008060 -7.885446e-04 0.000035 -0.000100
smoke -0.000789 8.103736e-03 0.000485 0.000492
male 0.000035 4.848158e-04 0.008091 -0.000219
race_Hispanic -0.000100 4.924759e-04 -0.000219 0.015657
race_Other -0.000769 3.214313e-04 0.000412 0.007145
race_White 0.000502 6.153204e-04 0.000814 0.007237
education_K-8 -0.000009 1.486314e-04 0.000085 -0.000140
education_Some college -0.000223 2.258767e-04 -0.000302 -0.000318
covariate race_Other race_White education_K-8 \
covariate
age -0.000051 -0.000036 0.000022
sbp -0.000019 0.000021 -0.000043
scr 0.000118 0.000219 -0.000194
bmi 0.000004 -0.000015 0.000050
hba1c 0.000133 0.000305 -0.000034
hypertension -0.000769 0.000502 -0.000009
smoke 0.000321 0.000615 0.000149
male 0.000412 0.000814 0.000085
race_Hispanic 0.007145 0.007237 -0.000140
race_Other 0.015080 0.007204 -0.000875
race_White 0.007204 0.015962 0.000017
education_K-8 -0.000875 0.000017 0.012373
education_Some college -0.001031 -0.000184 0.005783
covariate education_Some college
covariate
age -0.000008
sbp -0.000050
scr 0.000051
bmi 0.000059
hba1c -0.000319
hypertension -0.000223
smoke 0.000226
male -0.000302
race_Hispanic -0.000318
race_Other -0.001031
race_White -0.000184
education_K-8 0.005783
education_Some college 0.011580
Show code cell source
from lifelines import KaplanMeierFitter
import matplotlib.pyplot as plt
# Instantiate the KaplanMeierFitter
kmf = KaplanMeierFitter()
# Fit the data into the model
kmf.fit(df['time_to_failure'], event_observed=df['status'])
# Plot the Kaplan-Meier survival curve
plt.figure(figsize=(10, 6))
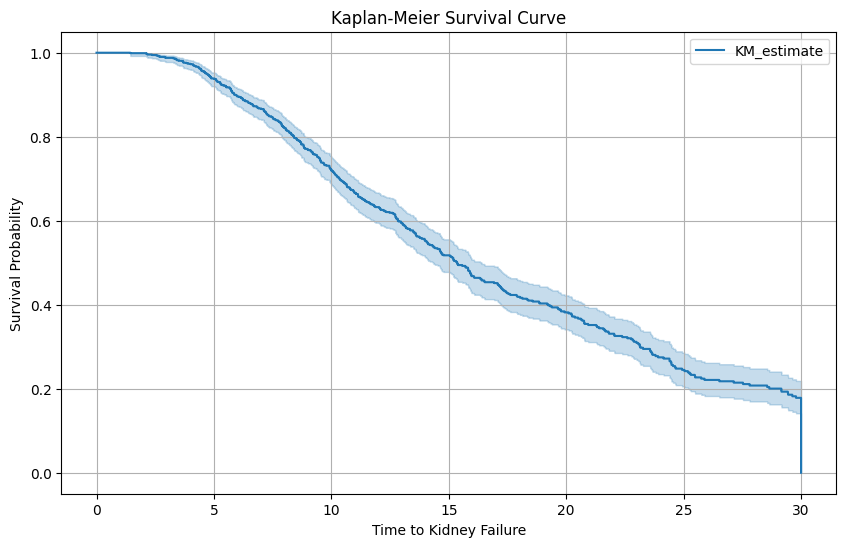
kmf.plot()
plt.title('Kaplan-Meier Survival Curve')
plt.xlabel('Time to Kidney Failure')
plt.ylabel('Survival Probability')
plt.grid(True)
plt.savefig('1_min_KM.png')
plt.show()
Show code cell source
from lifelines import KaplanMeierFitter
import matplotlib.pyplot as plt
# Instantiate the KaplanMeierFitter
kmf = KaplanMeierFitter()
# Fit the data into the model
kmf.fit(df['time_to_failure'], event_observed=df['status'])
# Get the survival function
survival_function = kmf.survival_function_
# Compute 1 minus the survival function
complement_survival_function = 1 - survival_function
# Plot the complement of the Kaplan-Meier survival curve
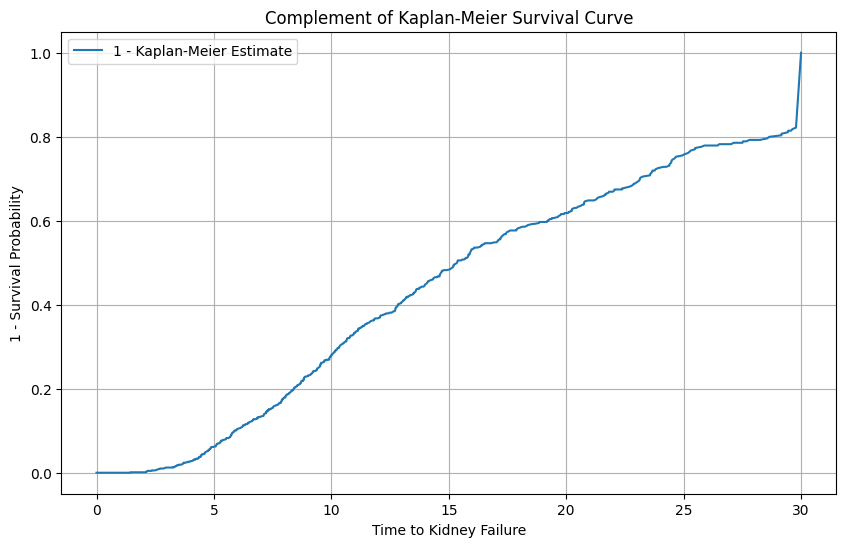
plt.figure(figsize=(10, 6))
plt.plot(complement_survival_function, label='1 - Kaplan-Meier Estimate')
plt.title('Complement of Kaplan-Meier Survival Curve')
plt.xlabel('Time to Kidney Failure')
plt.ylabel('1 - Survival Probability')
plt.legend()
plt.grid(True)
plt.savefig('1_min_KM.png')
plt.show()